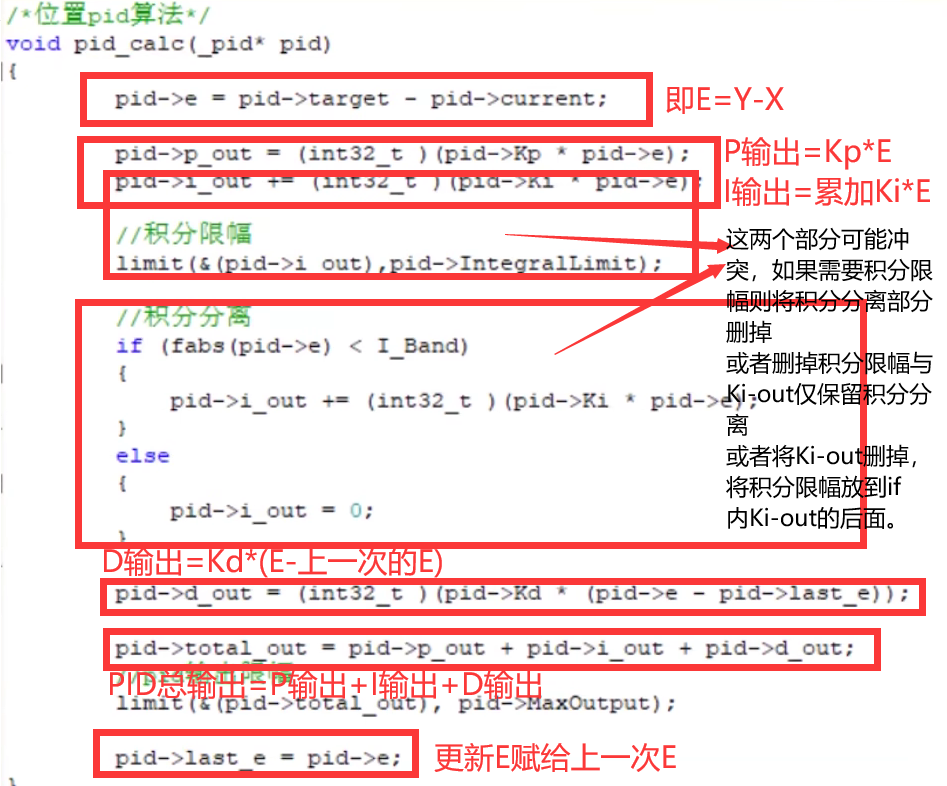
PID控制算法的使用非常广泛!
是电路控制中必学的算法。
# PID算法学习笔记
# 引入
PID控制算法是结合比例、积分和微分三种环节于一体的控制算法,它是连续系统中技术最为成熟、应用最为广泛的一种控制算法,该控制算法出现于20世纪30至40年代,适用于对被控对象模型了解不清楚的场合。
实际运行的经验和理论的分析都表明,运用这种控制规律对许多工业过程进行控制时,都能得到比较满意的效果。PID控制 的实质就是根据输入的偏差值,按照比例、积分、微分的函数关系进行运算,运算结果用以控制输出。
# 适用系统
满足线性高斯系统
线性高斯性:
- 1、齐次性: ky=f(kx)
- 2、叠加性: y1+y2=f(x1)+f(x2)=f(x1+x2)
- 高斯性:噪声满足正太分布

# 细化适用系统
准确地来说是适用二阶以内的线性系统(数学表达如图)
 卡尔曼滤波视频链接 (opens new window)
卡尔曼滤波视频链接 (opens new window)
- 一阶系统举例
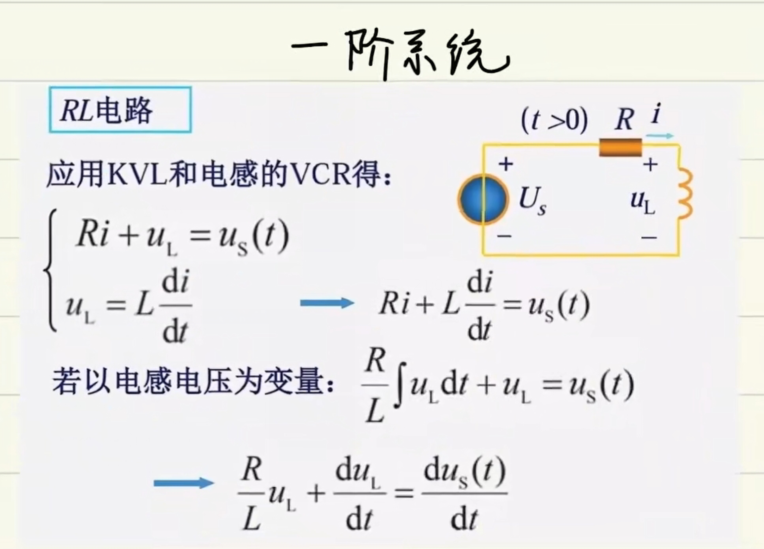
- 二阶系统举例
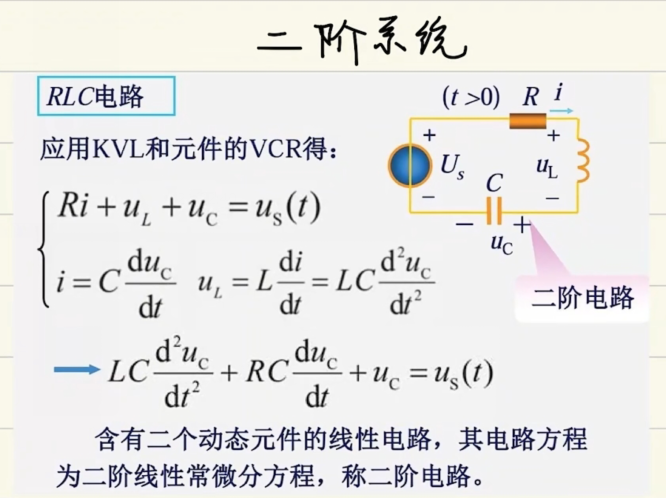
- 高阶系统若可以简化为二阶系统有可能适用PID算法
- 非线性系统通过李雅普诺夫定理 (opens new window)在非线性系统平衡点处线性化也可能适用PID算法。
# 原理
来自百度百科-PID算法 (opens new window)
# PID控制原理
闭环控制是根据控制对象输出反馈来进行校正的控制方式,它是在测量出实际与计划发生偏差时,按定额或标准来进行纠正的。比如控制一个电机的转速,就得有一个测量转速的传感器,并将结果反馈到控制路线上。提到闭环控制算法,不得不提PID,它是闭环控制算法中最简单的一种。PID是比例 (Proportion) 积分 ,(Integral) 微分 ,(Differential coefficient) 的缩写,分别代表了三种控制算法。通过这三个算法的组合可有效地纠正被控制对象的偏差,从而使其达到一个稳定的状态。
# PID参数调节
在整定PID控制器参数时,可以根据控制器的参数与系统动态性能和稳态性能之间的定性关系,用实验的方法来调节控制器的参数。有经验的调试人员一般可以较快地得到较为满意的调试结果。在调试中最重要的问题是在系统性能不能令人满意时,知道应该调节哪一个参数,该参数应该增大还是减小。
# 开环控制系统
# 一般开环控制系统框图
如:水流量控制开关
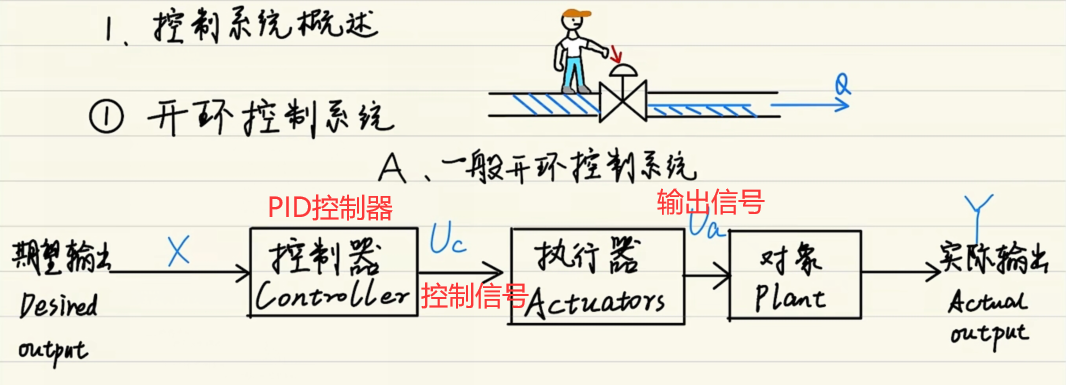
缺点:
无反馈,导致无法自动调节。
# 前馈控制系统框图
如:水流量控制开关
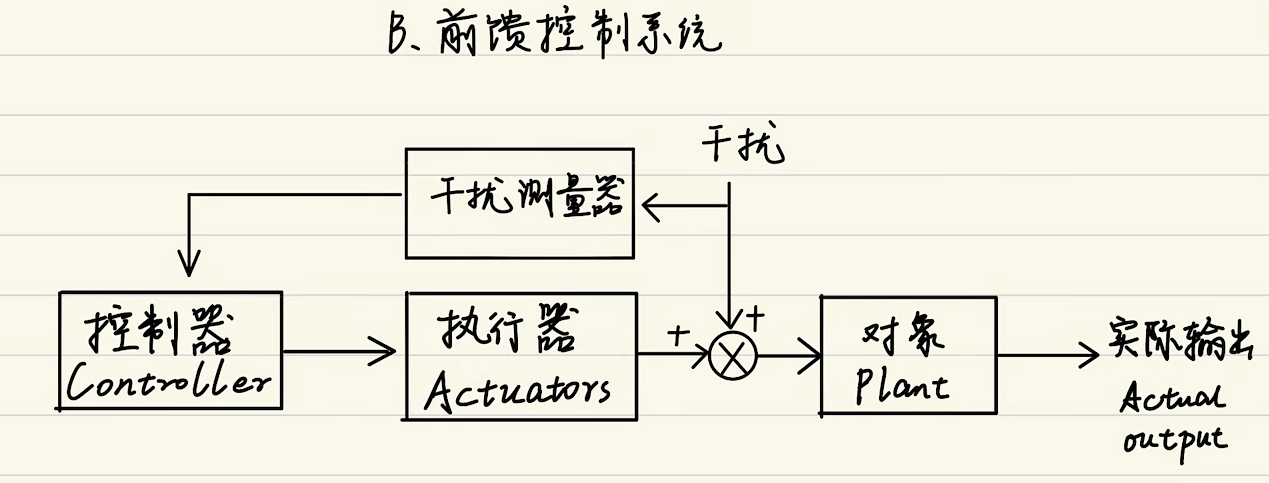
若不存在干扰则直接作用于对象。若有干扰则检测干扰,利用控制器计算出补偿然后输出给执行器再作用到对象。
# 闭环控制系统
# 单闭环
如:水流量控制开关
系统框图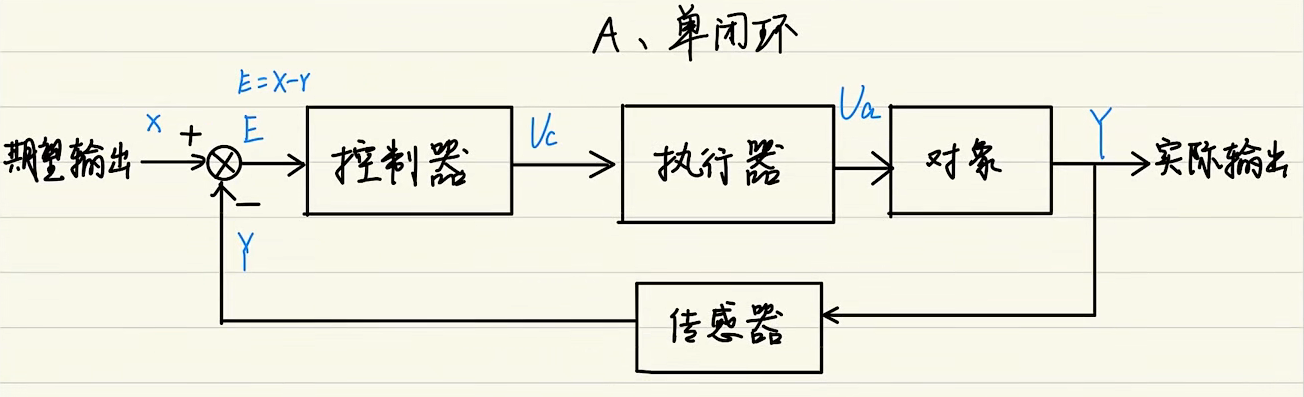
与一般开环系统多一个反馈。
# 双闭环
如:水位控制开关
系统框图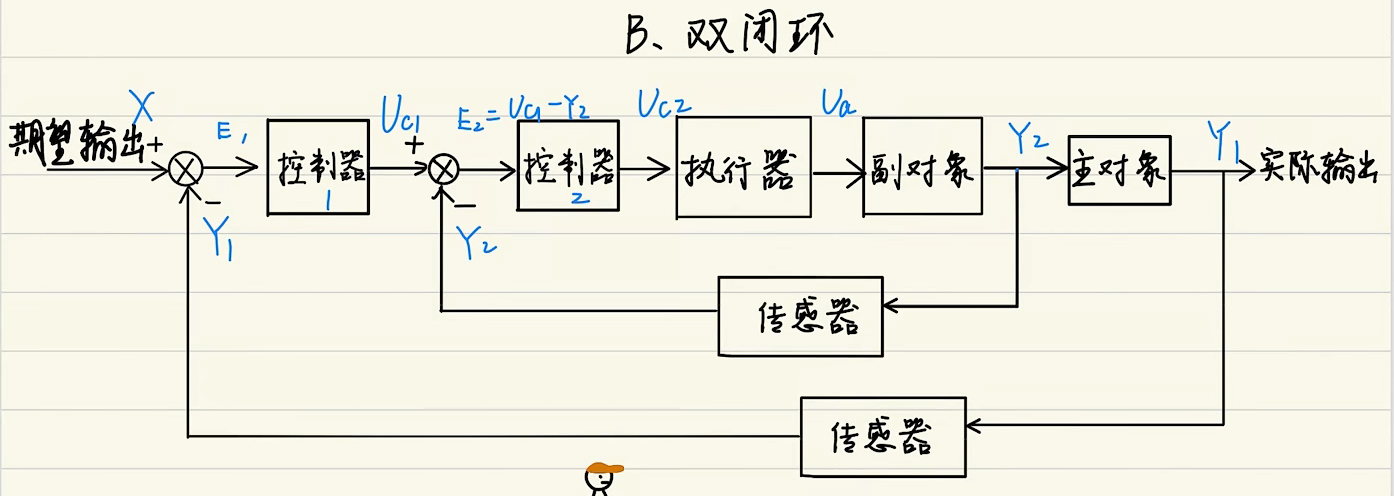
与一般单闭环控制系统多一个闭环,外层的环叫外环,内层叫内环。
传感器是人的眼睛,观察反馈信息,控制器1为人脑,根据水位变化做出计算。
控制器2也为人脑,用于做其他任务(运算)。
执行器是水阀,直接控制副对象(管道),进而影响水箱(主对象)。
控制过程
以下图为例
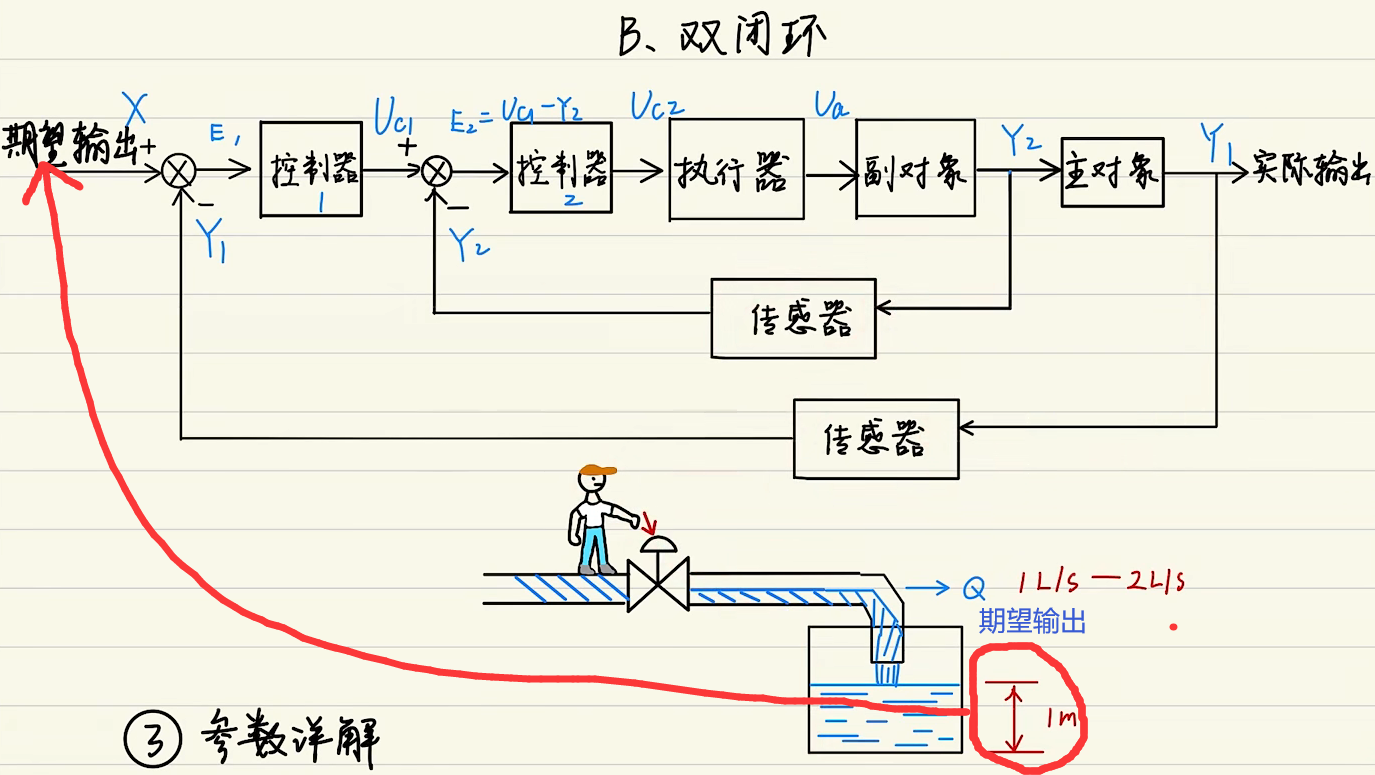
水位1m为我们的期望输出,与我们实际输出作差后得到E1,利用E1输入控制器控制再与实际流量做差,经过运算得到E2,最终决定水管加大/减小。做出执行后,作用给副对象。
优缺点:可以控制内环的流量,但流量是随动的,可能会在1L/s~2L/s变化,可以加快对水位的控制。利用内环控制稳定性,则外环控制起来会方便很多。
# 复合控制系统
前馈-反馈符合控制系统
系统框图如下
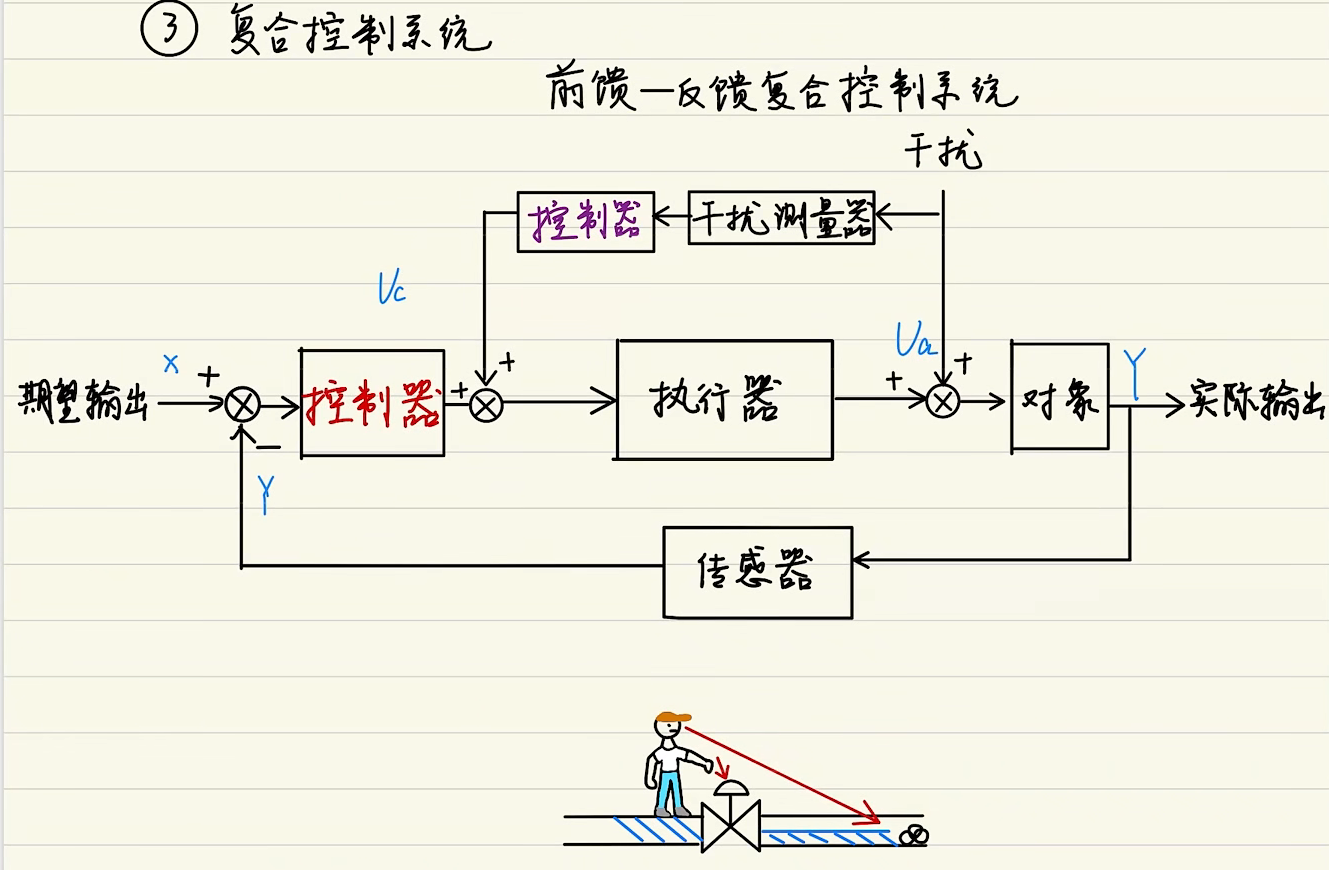
框图解释:
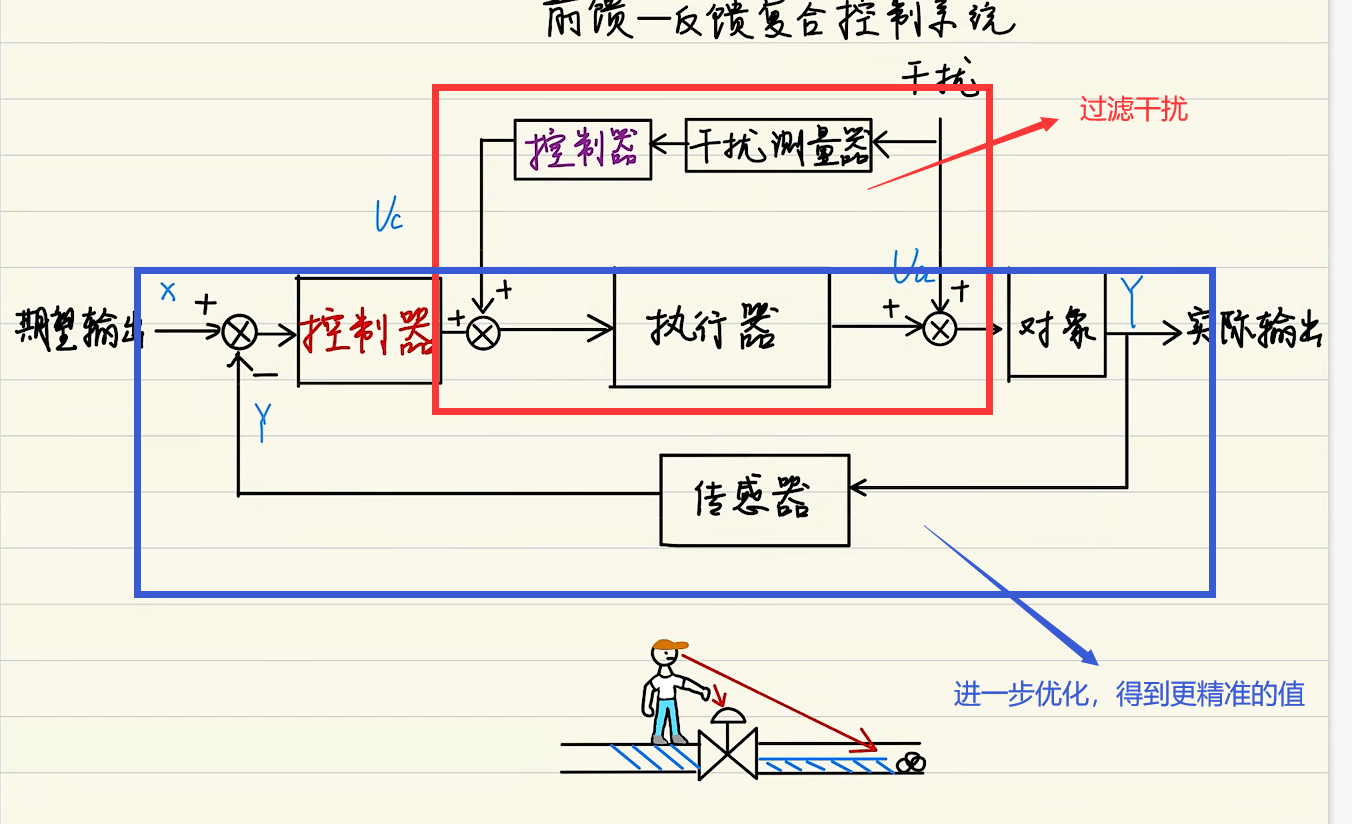
前馈环(上方的环)作补偿即过滤干扰。反馈环根据实际的流量对系统做出反馈进行必要的补偿。
# 参数详解
# 误差
期望输出-实际输出
# 控制器输出
控制器经过对E的处理(PID运算)得到的值。
# 执行器输出
直接作用到对象的输出(对应图中就是阀门打开的大小)
# 系统输出
即为实际输出
# 连续与离散信号
1、图形表示
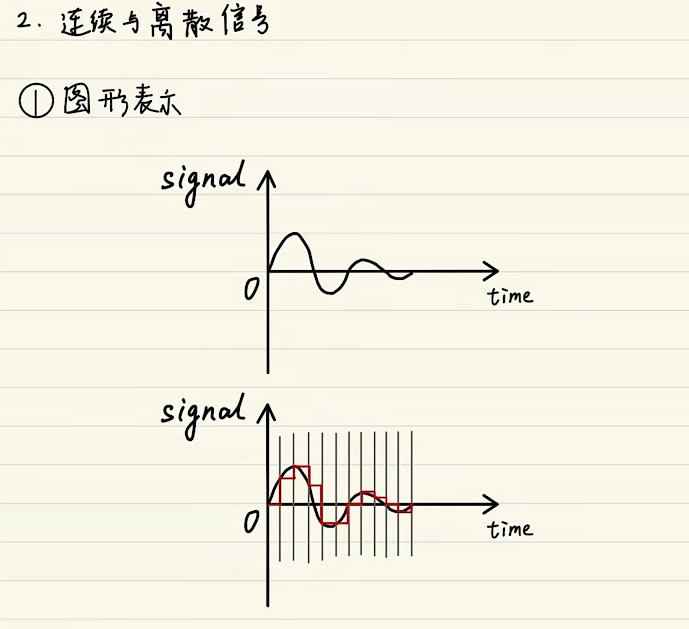
2、数学表达式

- 积分是信号的表达式;
- 连续信号微分为离散信号表达
# PID理论学习
# PID公式
# 抽象派(教科书式)
数学公式如图所示:

C为输出,e为误差,P为比例度,Ti为时间积分时间,Td为微分时间。p/i/d为我们所需调节的参数。
但在实际使用(计算机内使用)会归一化
即以上连续PID公式和离散PID公式。换之为调Kp、Ki、Kd三个参数(系数)。
离散PID公式将△t归一化得到以下公式
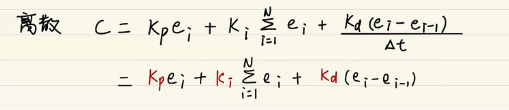
# PID形象解释
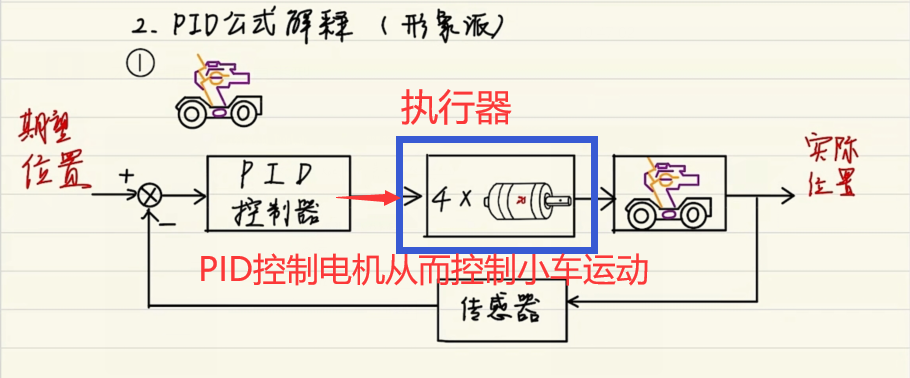
P的控制作用 实例:
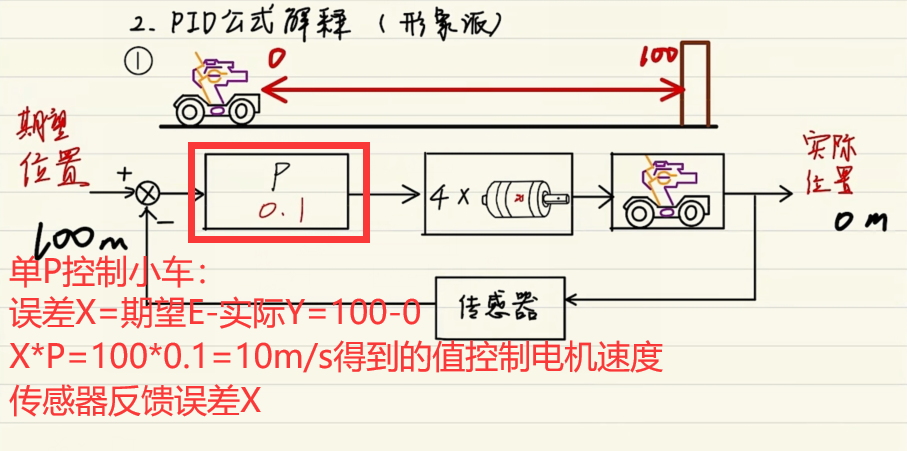
在小车控制系统中,P主要控制小车驱动(速度)
此时,小车距离与速度变化曲线图
可见,P只能无限接近期望值,不会完全等于期望值。
P控制产生的实际值与期望值的误差称稳态误差i的控制作用
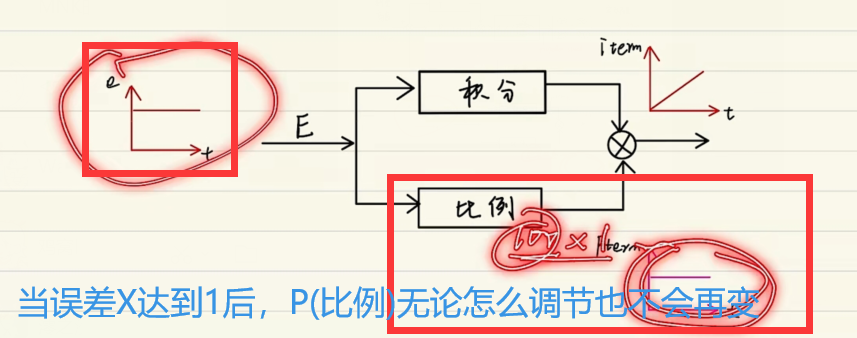
当误差达到1时P(比例)项不会再变,因此无法达到预期值。
i提供积分作用,使误差1无限接近0最终达到预期。
但PI调节到误差为0时,P得到的值为0,不再提供动力。
但I值不会因P值改变而收到影响,只会停止积累误差,可实现无人机悬停。
示意图: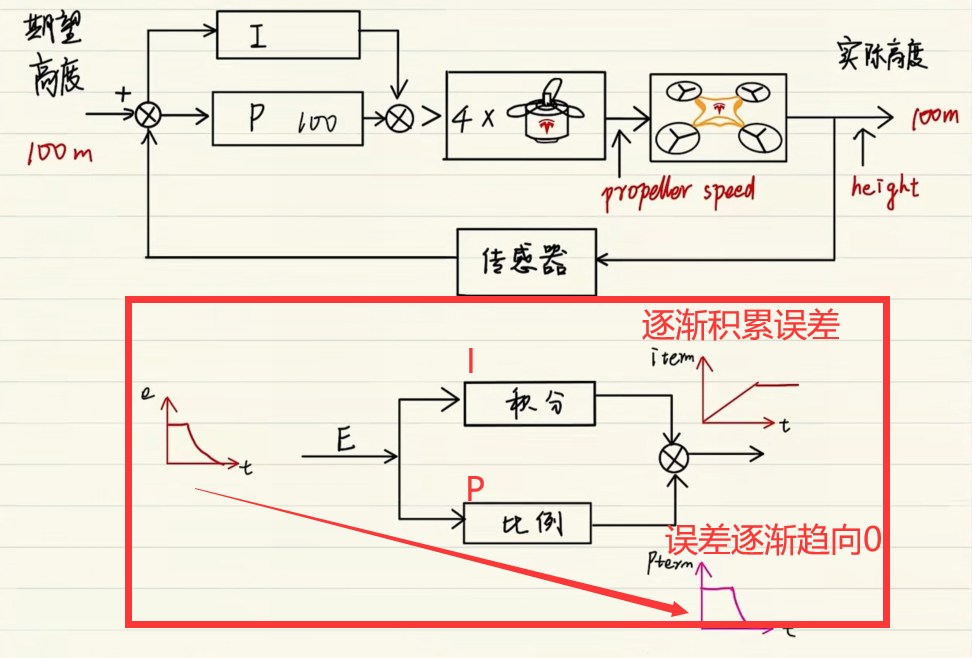
d的控制系统
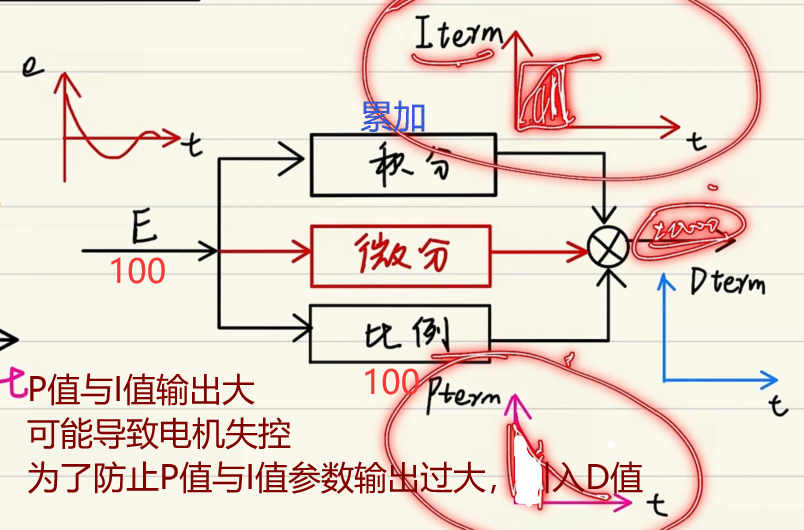
前段区域P项与I项过大的输出可能会瞬间超过预期,为防止此情况发生引入D。
D项给负的信号输出,防止误差小于0。
PID综合示意图: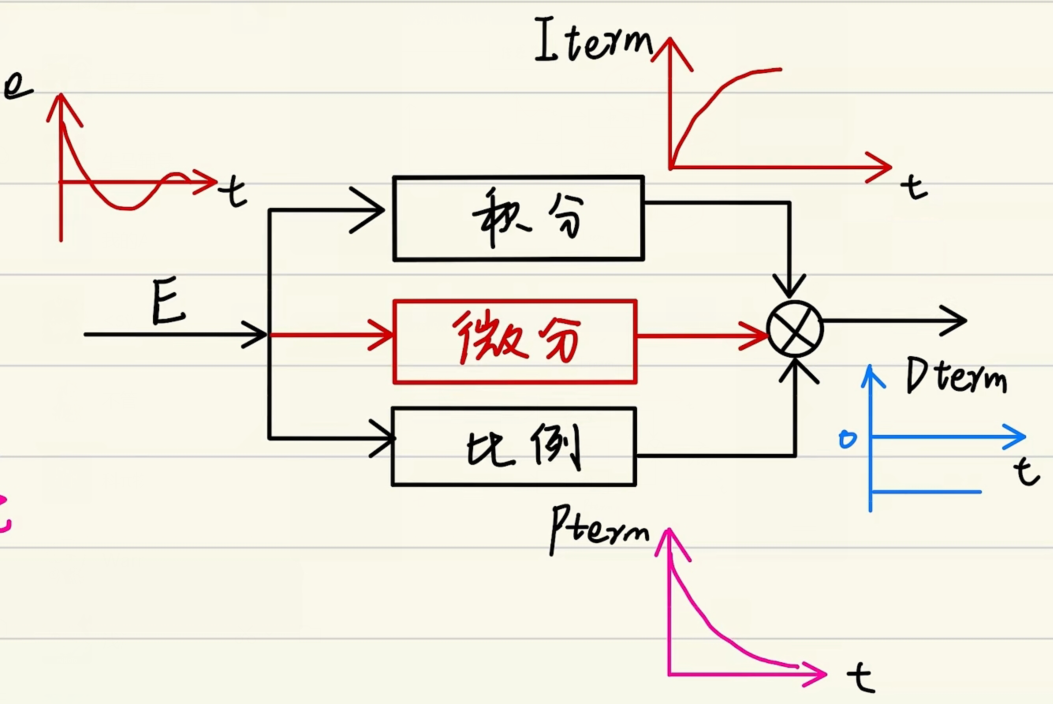
# 调参
调参示意图:
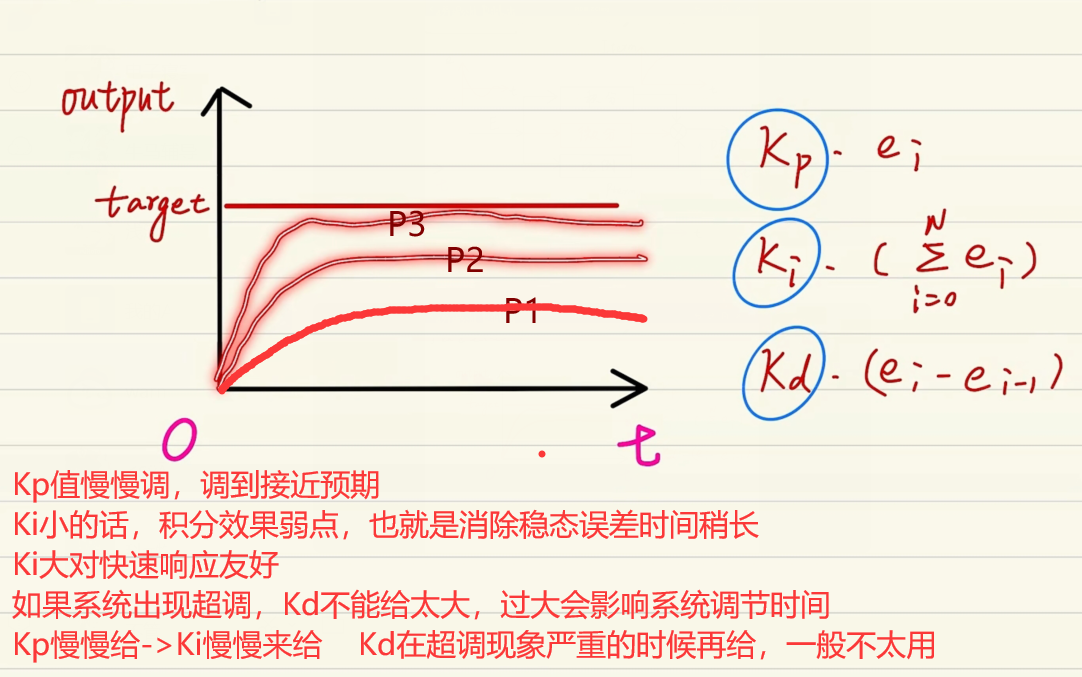
# 补充相关控制知识
# 积分限幅
先上图
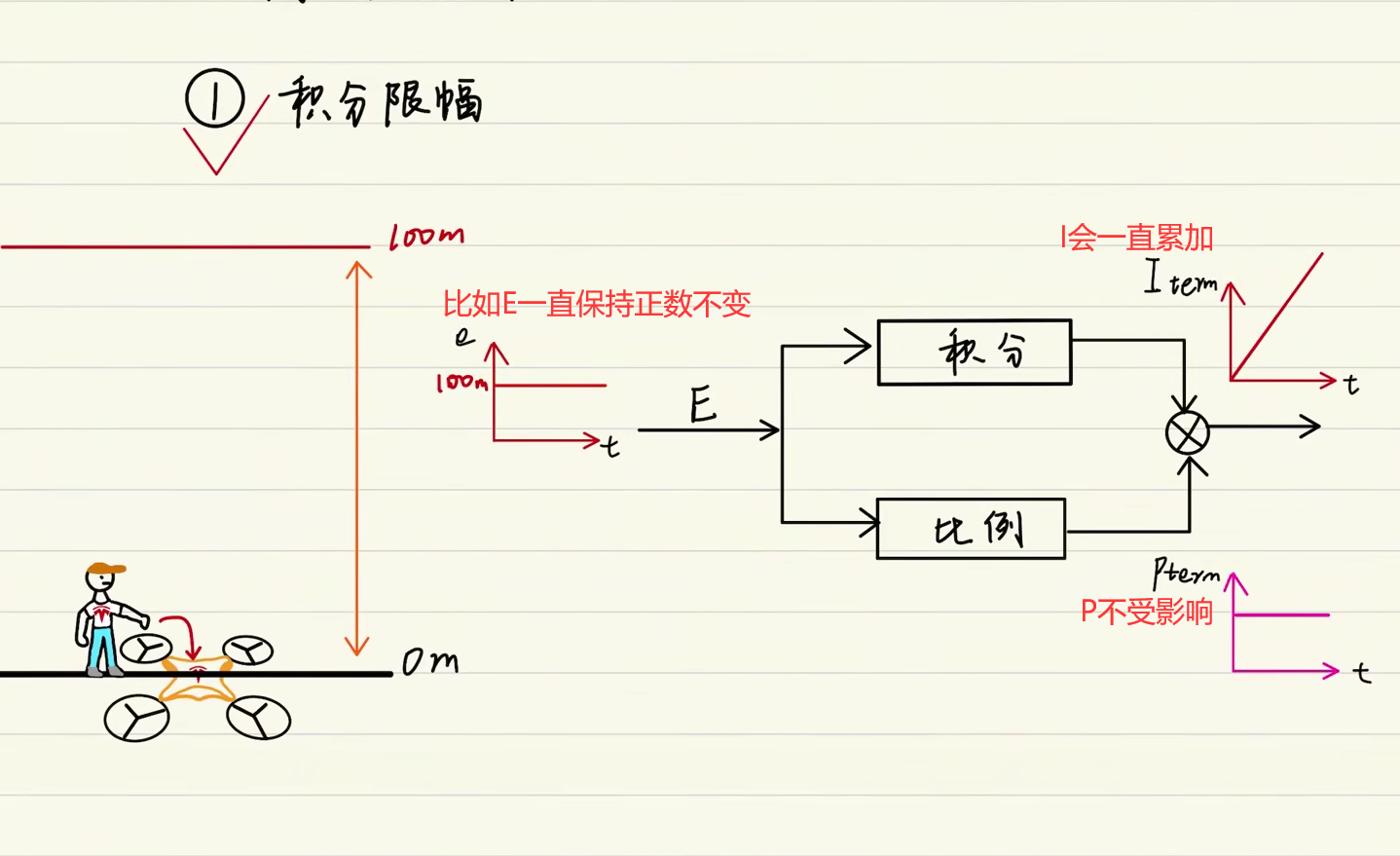
当E不变时P不受影响,为了防止PID输出过大,需要对I进行限幅。
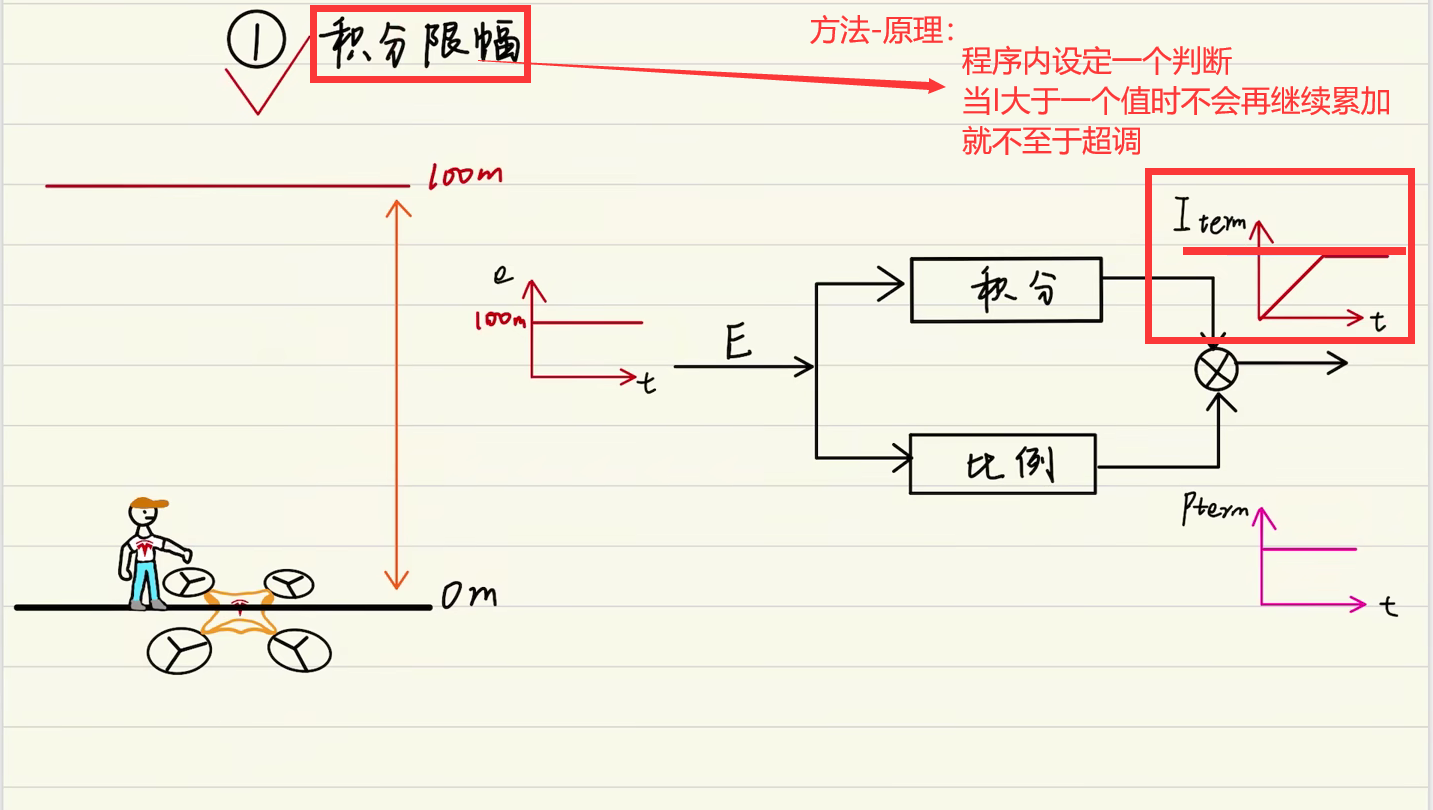
在程序内设定一个固定值,防止I过大,以至不会超调货超调幅度不大。
# 积分分离
当目标值增大时E会增大,如果E增大的值很大的话,P与I同时作用会导致PID总输出值过大而导致系统超调
为了防止此情况,我们需要对其进行积分分离
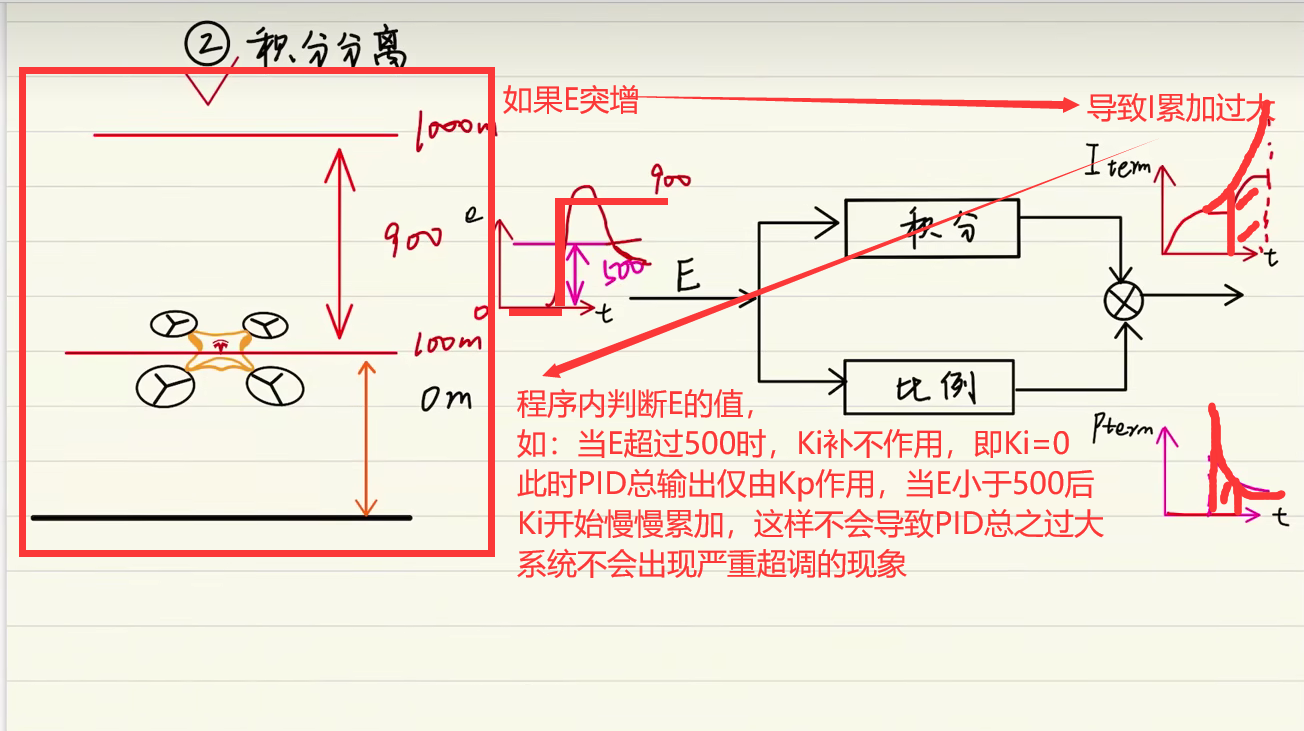
在程序内判断E的值,
例:当目标值突增,E大于500时,Ki影响极大,所以我们不将Ki启用,即Ki=0
此时PID总输出仅有Kp作用,到E小于500后Ki慢慢累加,系统输出由Ki与Kp作用。
这样可以防止系统超调。
# 实践
控制框图
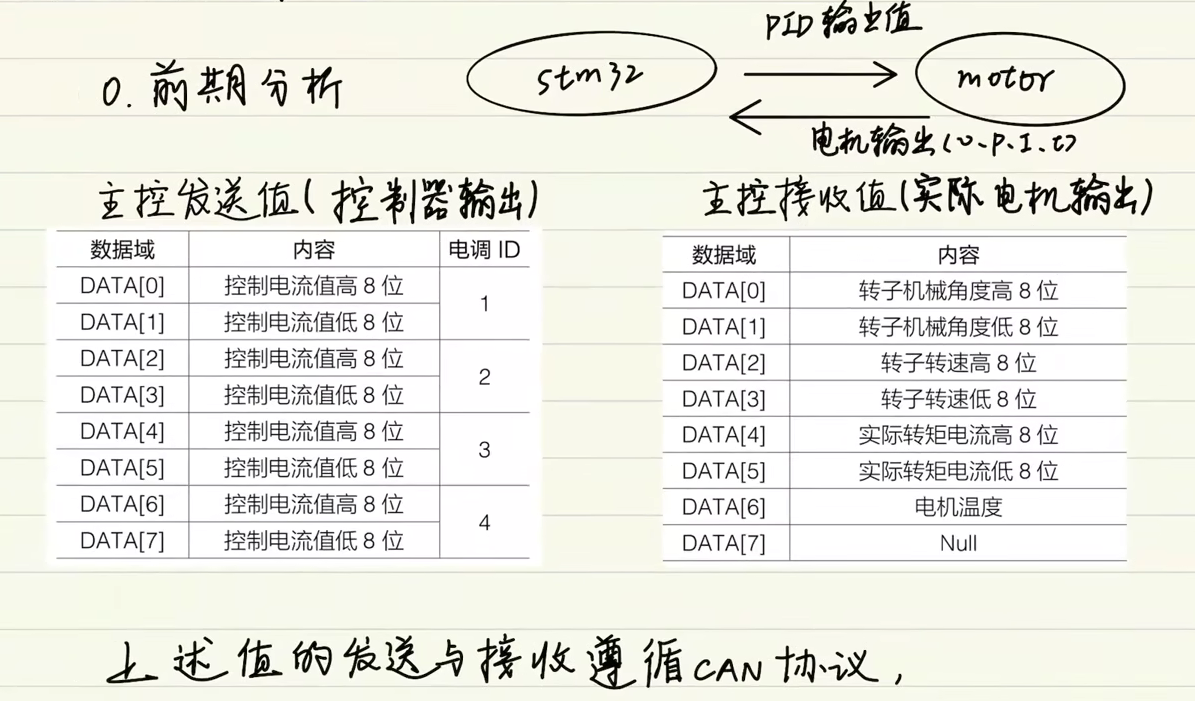
主控发送值->PID输出值 遵循C620电调协议(CAN协议-控制器局域网络)
补充
CAN总线网络主要挂在CAN_H和CAN_L,各个节点通过这两条线实现信号的串行差分传输,为了避免信号的反射和干扰,还需要在CAN_H和CAN_L之间接上120欧姆的终端电阻.
更多详解可以参照 CAN总线协议 (opens new window)
下图
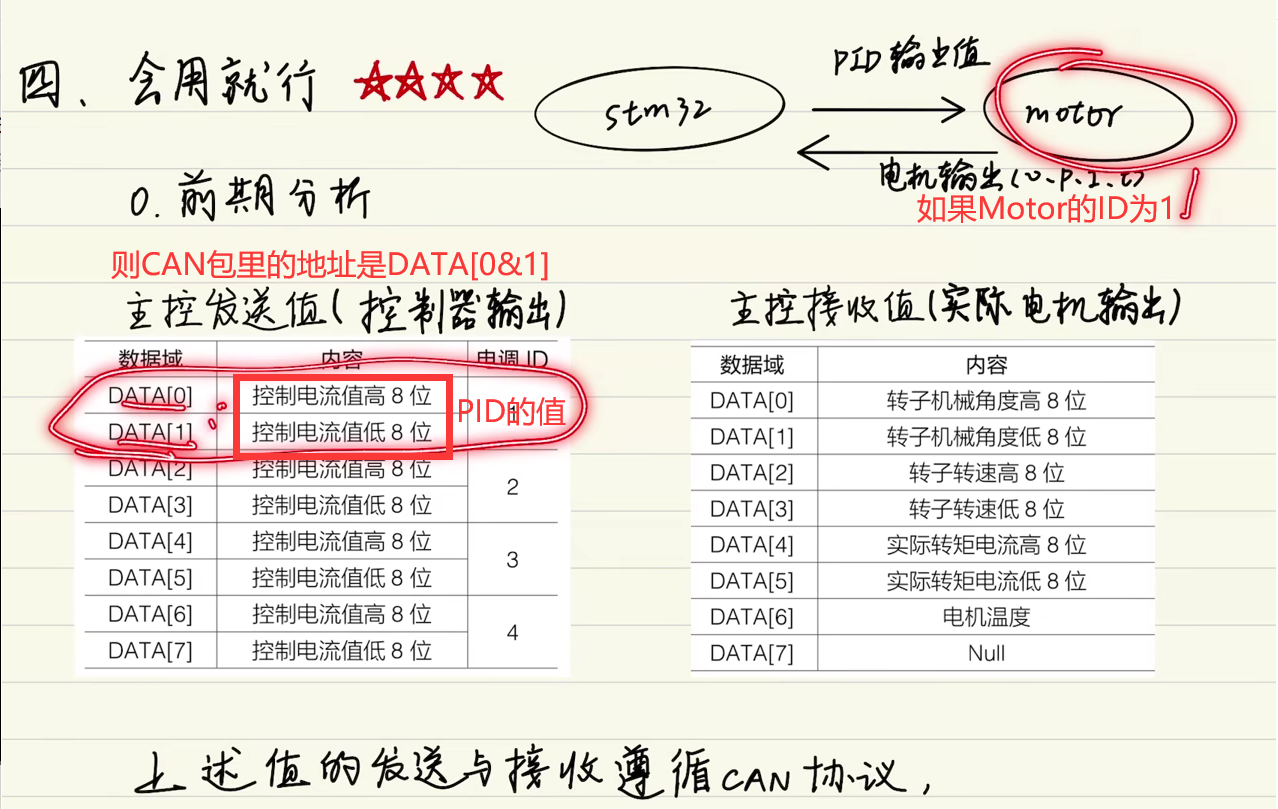 如果设Motor的ID为1,则CAN包内的0、1字节为PID的输出值
如果设Motor的ID为1,则CAN包内的0、1字节为PID的输出值
实际控制过程如下:
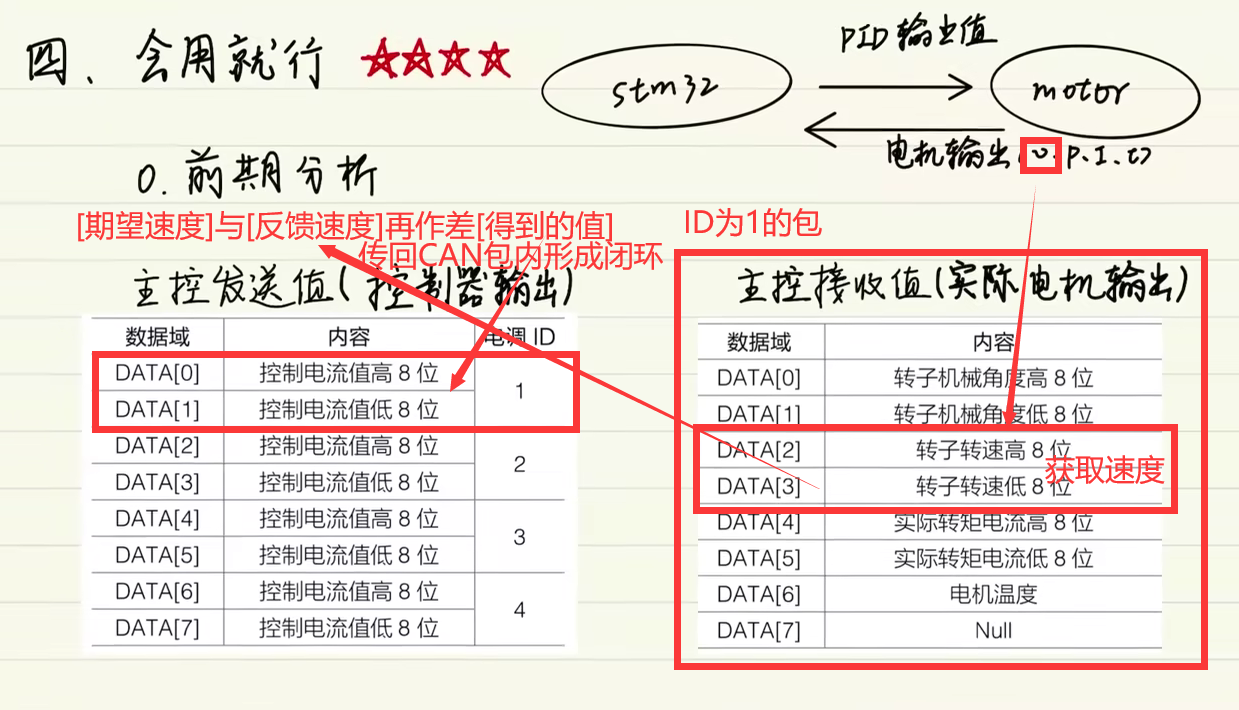
id1的包反馈数据里面包含一些数据,通过提取其中的速度(即PID的实际输出)传回主控
主控将期望与反馈回来的速度作差再传入CAN包DATA0与DATA1形成闭环。
# 代码实例